Orbits
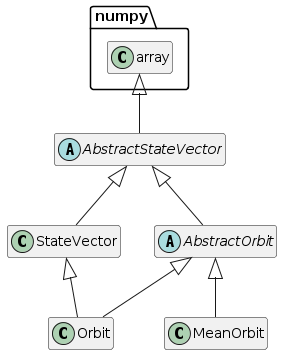
Abstract classes
- class beyond.orbits.statevector.AbstractStateVector(coord, date, form, frame, **kwargs)
Coordinate representation
- static __new__(cls, coord, date, form, frame, **kwargs)
- as_frame(name, **kwargs)
Register the orbit as frame.
see
beyond.frames.frames.orbit2frame()for details of the arguments
- as_orbit(propagator)
Attach a propagator to a StateVector, creating a new Orbit object
- Parameters:
propagator (Propagator) –
- Returns:
New Orbit object, with the same state as the creating StateVector
- Return type:
- copy(*, frame=None, form=None, same=None)
Provide a new object of the same point in space-time. Optionally, allow for frame and form conversion
- Keyword Arguments:
frame (str or Frame) – Frame to convert the new instance into
form (str or Form) – Form to convert the new instance into
same (StateVector) – A statevector from which to copy the frame and form
- Return type:
If the argument same is used, it overwrites frame and form.
Example:
# New instance of the same statevector sv1 = sv.copy() # statevector converted into spherical form sv2 = sv.copy(form="spherical") # statevector converted into EME2000 frame, keplerian form sv3 = sv.copy(form="keplerian", frame="EME2000") # statevector in the same frame and form as sv3 (EME2000, keplerian) sv4 = sv.copy(same=sv3)
Override
numpy.ndarray.copy()to include additional fields
- property cov
6x6 Covariance matrix
If a statevector and its covariance are expressed in the same frame, changing the frame of the statevector will trigger the change of its covariance frame.
- Type:
- property form
Form of the coordinates of the orbit If set as a string (e.g.
"cartesian") will be automatically converted to the corresponding Form object.orbit.form = "cartesian" # is equivalent to from beyond.orbits.forms import CART orbit.form = CART
- Type:
- property frame
Reference frame of the orbit If set as a string (e.g.
"EME2000") will be automatically converted to the corresponding Frame object.orbit.frame = "EME2000" # is equivalent to from beyond.frames.frames import EME2000 orbit.frame = EME2000
- Type:
- property maneuvers
Maneuver descriptions usable by the propagator. Not all propagators can handle maneuvers. Check their respective documentations for more details.
- Type:
list of
Man
- class beyond.orbits.orbit.AbstractOrbit(coord, date, form, frame, propagator, **kwargs)
Extrapolable coordinates (i.e. a
StateVectorassociated to aPropagatorvia thepropagate()method)- static __new__(cls, coord, date, form, frame, propagator, **kwargs)
- Parameters:
coord (list) – 6-length state vector
date (Date) – Date associated with the state vector
form (str or Form) – Name of the form of the state vector
frame (str or Frame) – Name of the frame of reference of the state vector
propagator (str or Propagator) – Name of the propagator to be used to extrapolate
- as_frame(name, **kwargs)
Register the orbit as frame.
see
beyond.frames.frames.orbit2frame()for details of the arguments
- ephem(**kwargs)
Tabulation of Orbit at a given step and on a given date range
- ephemeris(**kwargs)
Generator giving the propagation of the orbit at different dates
- iter(**kwargs)
see
Propagator.iter()
- property propagator
Propagator of the orbit. If set as a string (e.g.
"Sgp4") will be automatically converted to the corresponding propagator class and instantiated without arguments.- Type:
Concrete classes
- class beyond.orbits.statevector.StateVector(coord, date, form, frame, **kwargs)
Bases:
AbstractStateVectorRepresents a coordinate in time and space
- to_mean_orbit(propagator)
- Parameters:
propagator (AnalyticalPropagator) –
- Returns:
- MeanOrbit object which, when propagated at the same date,
returns the input StateVector
- Return type:
- class beyond.orbits.orbit.Orbit(coord, date, form, frame, propagator, **kwargs)
Bases:
StateVector,AbstractOrbitOsculating orbit, associated with a numerical propagator
- class beyond.orbits.orbit.MeanOrbit(coord, date, form, frame, propagator, **kwargs)
Bases:
AbstractOrbitMean orbit associated with a mean propagator
Forms
When using a StateVector or Orbit object it is possible
to change its form by naming the desired new form.:
>>> print(repr(orb))
Orbit =
date = 2020-10-04T04:38:08.250720 UTC
form = tle
frame = TEME
propag = Sgp4
coord =
i = 0.9013630748877075
Ω = 2.951400634341467
e = 0.0001204
ω = 1.769838910680086
M = 0.9752533341001394
n = 0.0011263401984422173
>>> orb.form = "keplerian_circular"
>>> print(repr(orb))
Orbit =
date = 2020-10-04T04:38:08.250720 UTC
form = keplerian_circular
frame = TEME
propag = Sgp4
coord =
a = 6798290.45301548
ex = -2.3806801365162165e-05
ey = 0.00011802286307643835
i = 0.9013630748877075
Ω = 2.951400634341467
u = 2.74529160645093
Some forms have aliases:
circularpoints tokeplerian_circular
meanpoints tokeplerian_mean
mean_circularpoints tokeplerian_mean_circular
eccentricpoints tokeplerian_eccentric
It is also possible to access individual element of a StateVector or
Orbit object by attribute or key. Some elements have aliases,
particularly those with Greek letters name:
>>> orb.Omega # is equivalent to orb.Ω
2.951400634341467
>>> orb["Omega"]
2.951400634341467
>>> orb.aol # is equivalent to orb.u
2.74529160645093
- class beyond.orbits.forms.Form(name, param_names)
Bases:
NodeBase class for orbital form definition
- beyond.orbits.forms.CART = <Form 'cartesian' at '0x7fc4a5015bb0'>
Cartesian form
- beyond.orbits.forms.KEPL = <Form 'keplerian' at '0x7fc4a5015af0'>
The keplerian form is
a : semi-major axis
e : eccentricity
i : inclination
Ω : right-ascension of ascending node (aliases : Omega, raan)
ω : Argument of perigee (alias : omega)
ν : True anomaly (alias : nu)
see wikipedia for details
- beyond.orbits.forms.SPHE = <Form 'spherical' at '0x7fc4a5015b50'>
Spherical form
r : radial distance / altitude
θ : azimuth / longitude (alias : theta)
φ : elevation / latitude (alias : phi)
r_dot : first derivative of radial distance / altitude
θ_dot : first derivative of azimuth / longitude (alias : theta_dot)
φ_dot : first derivative of elevation / latitude (alias : phi_dot)
- beyond.orbits.forms.TLE = <Form 'tle' at '0x7fc4a5015970'>
TLE special form
i : inclination
Ω : right-ascension of ascending node (aliases: Omega, raan)
e : eccentricity
ω : argument of perigee (alias : omega)
M : mean anomaly
n : mean motion
see
Tlefor details
- beyond.orbits.forms.KEPL_M = <Form 'keplerian_mean' at '0x7fc4a5015a90'>
Same as Keplerian, but replaces True anomaly with Mean anomaly
- beyond.orbits.forms.KEPL_C = <Form 'keplerian_circular' at '0x7fc4a50159d0'>
Special case for near-circular orbits
a : semi-major axis
ex : e * cos(ω)
ey : e * sin(ω)
i : inclination
Ω : right-ascension of ascending node (aliases : Omega, raan)
u : true argument of latitude u = ω + ν (alias : aol)
- beyond.orbits.forms.KEPL_E = <Form 'keplerian_eccentric' at '0x7fc4a5015a30'>
Same as Keplerian, but replaces True anomaly with Eccentric anomaly
- beyond.orbits.forms.KEPL_MC = <Form 'keplerian_mean_circular' at '0x7fc4a5015cd0'>
Same as Circular but with mean argument of latitude
a : semi-major axis
ex : e * cos(ω)
ey : e * sin(ω)
i : inclination
Ω : right-ascension of ascending node (aliases : Omega, raan)
α : mean argument of latitude α = ω + M (aliases : alpha, maol)
- beyond.orbits.forms.EQUI = <Form 'equinoctial' at '0x7fc4a5015c10'>
The Equinoctial form is
a : semi-major axis
ex : first element of the eccentricity vector
ey : second element of the eccentricity vector
ix : first element of the inclination vector
iy : second element of the inclination vector
l : argument of longitude
This form is not subject to ambiguity when the orbit is circular and/or equatorial like the keplerian form is (on ω and Ω, respectively)
- beyond.orbits.forms.CYL = <Form 'cylindrical' at '0x7fc4a5015c70'>
Cylindrical form
r : radial distance
θ : azimuth (alias : theta)
z : height
r_dot : first derivative of radial distance / altitude
θ_dot : first derivative of azimuth / longitude (alias : theta_dot)
vz : velocity along z
OrbitInfos
- class beyond.orbits.statevector.Infos(orb)
Compute additional informations on an orbit
- property apocenter
Radius of the apocenter
- property delay
Light propagation delay from the point in space described by
selfto the center of the reference frame- Type:
timedelta
- property dinf
Distance between the focus and the asymptote
- property elliptic
True if the orbit it elliptic
- property energy
Mechanical energy of the orbit
- property fpa
Flight path angle
- property hyperbolic
True if the orbit it hyperbolic
- property n
Mean motion
- property parabolic
True if the orbit it parabolic
- property pericenter
Radius of the pericenter
- property period
Period of the orbit as a timedelta
- property r
Instantaneous radius
- property ra
Radius of the apocenter
- property rp
Radius of the pericenter
- property v
Instantaneous velocity
- property va
Velocity at apocenter
- property vinf
Hyperbolic excess velocity
- property vp
Velocity at pericenter
- property za
Altitude of the apocenter, relative to the body equatorial surface
- property zp
Altitude of the pericenter, relative to the body equatorial surface
Ephem
Definition of ephemeris
- class beyond.orbits.ephem.Ephem(orbits, method=None, order=None)
This class represents a range of orbits
It provides several useful interfaces in order to compute through them
Example:
ephem = orb.ephem(Date.now(), timedelta(hours=6), timedelta(minutes=2)) ephem.frame = 'ITRF' ephem.form = 'spherical' latitudes = ephem[:,1] longitudes = ephem[:,2]
- as_frame(name, **kwargs)
Register the Ephem object as a frame
see
beyond.frames.frames.orbit2frame()for details of the arguments
- copy(*, form=None, frame=None, same=None)
Create a deep copy of the ephemeris. Optionally, allow frame and form changing
- Keyword Arguments:
form (str or Form) – Form to convert the new instance into
frame (str or Frame) – Frame to convert the new instance into
same (StateVector) – A statevector from which to copy the frame and form
- Returns:
New ephemeris object
- Return type:
If the argument same is used, it overwrites frame and form.
Example:
# New instance of the same ephemeris e1 = e.copy() # ephemeris converted into spherical form e2 = e.copy(form="spherical") # ephemeris converted into EME2000 frame, keplerian form e3 = e.copy(form="keplerian", frame="EME2000") # ephemeris in the same frame and form as e3 (EME2000, keplerian) e4 = e.copy(same=sv3)
Override
numpy.ndarray.copy()to include additional fields
- property dates
Generator yielding Dates of each Orbit object of the ephem
- ephem(*args, **kwargs)
Create an Ephem object which is a subset of this one
Take the same keyword arguments as
ephemeris()- Return type:
- ephemeris(*args, **kwargs)
Same as
self.iter()Implemented to expose the same methods as
Orbit
- property form
Get the form of the first point
- property frame
Get the frame of the first point
- property interp
Interpolator object. Callable
- interpolate(date)
Interpolate data at a given date
- iter(*, dates=None, start=None, stop=None, step=None, strict=True, **kwargs)
Ephemeris generator based on the data of this one, but with different dates
- Keyword Arguments:
dates (list of
Date) – Dates from which iterate overstart (Date or None) – Date of the first point
stop (Date, timedelta or None) – Date of the last point
step (timedelta or None) – Step to use during the computation. Use the same step as self if None
listeners (list of:py:class:~beyond.orbits.listeners.Listener) –
strict (bool) – If True, the method will return a ValueError if
startorstopis not in the range of the ephemeris. If False, it will take the closest point in each case.
- Yields:
Orbit- Raises:
ValueError –
There is two ways to use the iter() method.
If dates is defined, it should be an iterable of dates. This could be a generator as per
Date.range, or a list.# Create two successive ranges of dates, with different steps dates = list(Date.range(Date(2019, 3, 23), Date(2019, 3, 24), timedelta(minutes=3))) dates.extend( Date.range(Date(2019, 3, 24), Date(2019, 3, 25), timedelta(minutes=10), inclusive=True) ) ephem.iter(dates=dates)
The alternative, is the use of start, stop and step keyword arguments which work exactly as
Date.range(start, stop, step, inclusive=True)If one of start, stop or step arguments is set to
Noneit will keep the same property as the generating ephemeris.# In the examples below, we consider the 'ephem' object to be an ephemeris starting on # 2017-01-01 00:00:00 UTC and ending and 2017-01-02 00:00:00 UTC (included) with a fixed # step of 3 minutes. # These two calls will generate exactly the same points starting at 00:00 and ending at # 12:00, as 12:02 does not fall on a date included in the original 'ephem' object. ephem.iter(stop=Date(2017, 1, 1, 12)) ephem.iter(stop=Date(2017, 1, 1, 12, 2)) # Similarly, these calls will generate the same points starting at 12:00 and ending at # 00:00, as 11:58 does not fall on date included in the 'ephem' object. ephem.iter(start=Date(2017, 1, 1, 11, 58)) ephem.iter(start=Date(2017, 1, 1, 12)) # This call will generate an ephemeris, wich is a subpart of the initial one ephem.iter(start=Date(2017, 1, 1, 8), stop=Date(2017, 1, 1, 16))
- propagate(date)
Alias of
interpolate()
- property start
Date of the first element
- property stop
Date of the last element
Maneuvers
- class beyond.orbits.man.ImpulsiveMan(date, dv, frame=None, comment=None)
Impulsive maneuver
- __init__(date, dv, frame=None, comment=None)
- Parameters:
date (Date) – Date of application of the maneuver
dv (list) – Vector of length 3 describing the velocity increment
frame (str) – Which frame is used for applying the increment :
'TNW','QSW'orNone. Ifframe = Nonethe same frame as the orbit is usedcomment (str) – Free text to give context on a given maneuver (‘apogee maneuver’, ‘inclination correction’)
- class beyond.orbits.man.KeplerianImpulsiveMan(date, *, da=0, di=0, dOmega=0, comment=None)
Impulsive maneuver directly modifying keplerian parameters changes
For maximum efficiency:
‘a’ should be modified at apoapsis or periapsis, via da
‘i’ should be modified at descending or ascending node, via di
‘Ω’ should be modified at argument of latitude +/- 90 deg, via dOmega
- class beyond.orbits.man.ContinuousMan(date, duration, *, dv=None, accel=None, date_pos='start', frame=None, comment=None)
Continuous thrust
- __init__(date, duration, *, dv=None, accel=None, date_pos='start', frame=None, comment=None)
- Parameters:
date (Date) – Date (see date_pos)
duration (timedelta) – Duration of the thrust
dv (list[float]) – Vector of length 3 describing the velocity increment (in m/s)
accel (list[float]) – Vector of length 3 describing the acceleration (in m/s²)
date_pos (str) – define the position of the date argument. Accepted values are
start,stop,medianframe (str) – frame of the maneuver
comment (str) –
Cov
- class beyond.orbits.cov.Cov(orb, values, frame)
Covariance matrix
- static __new__(cls, orb, values, frame)
Create a covariance matrix
- Parameters:
orb (StateVector) – State vector from which this is the covariance
values – 2D matrix (6x6)
frame (str) – Frame in which the covariance is expressed
Warning
For the time being, only 6x6 matrices are handled, but in the future there is no reason why NxN matrix can’t be used as well
- property frame
Frame of the covariance
When this value is changed, the covariance is converted. Accepted frames are regular frames (defined in Frames) and ‘TNW’ or ‘QSW’.
If the frame of this covariance is the same as its parent statevector/orbit, a change of its parent frame will trigger a change of this covariance frame as well.
orb.frame.name # "EME2000" orb.cov.frame.name # "EME2000" orb.frame = "ITRF" orb.frame.name # "ITRF" orb.cov.frame.name # "ITRF"
It it possible to untangle them by switching only the covariance to an other frame
orb.frame.name # "EME2000" orb.cov.frame.name # "EME2000" orb.cov.frame = "ITRF" orb.frame.name # "EME2000" orb.cov.frame.name # "ITRF"